Números ( I )

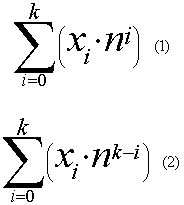¿Qué es un número?

Básicamente es un símbolo; y como tal representa algo. En este caso: una cantidad. Sin embargo, las cantidades posibles son infinitas por lo que crear infinitos símbolos es no sólamente inútil sino que también anti-educativo. Es por eso que se utilizan un número finito de símbolos bajo una serie de reglas; cada conjunto de símbolos con sus respectivas reglas se llama: Sistema de numeración.

(Acá necesito todavía un poco de investigación para agregar ejemplos de diferentes sistemas de numeración: Romana, Hindú, Egipcia, etc.)

Como ya dijimos, un sistema de numeración consta de una cantidad finita de símbolos e "instrucciones tal que se pueden formar todos los números con ellos. La cantidad de símbolos que utiliza un sistema de numeración se denomina base de dicho sistema. En la vida cotidiana estamos acostumbrados a trabajar con el Sistema Decimal, en Base 10 (0,1,2,3,4,5,6,7,8,9); las PCs utilizan Base 2 (0,1) - Sistema Binario - o Base 16 (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F) - Sistema Hexadecimal - pero puede utilizarse cualquier base que se quiera.

Estos sistemas se basan en la posición de cada símbolo para saber su valor. Por ejemplo: el 1 no es lo mismo en 01 que en 10. Ese valor no sólo depende de la posición en la que se encuentra el símbolo, sino también del sistema en el que se está trabajando. Por ejemplo: 1+1=2; y también podemos escribir 1+1=10 siempre aclaremos en qué sistema estamos trabajando. La última expresión sólo tiene sentido en un sistema de numeración con 2 símbolos y éstos sean {0,1} (en ese orden). Los sistemas con los que se trabajan comúnmente se denominan 'posicionales' y se basan en lo siguiente:

Si abcd es un número en base n (lo expresaremos como {abcd}_n ), entonces:
{abcd}_n = d*n^0 + c*n^1 + b*n^2 + a*n^3

Por ejemplo:
{2654}_10 4*10^0 + 5*10^1 + 6*10^2 + 2*10^3.

En general, un conjunto ordenado de k elementos tomados de n símbolos (Base n) expresa los números según la fórmula (1) que precede este post. Es la suma de cada uno de esos símbolos multiplicado por la base elevado a la posición en la que se ubica ese símbolo - de ahí la importancia que el conjunto sea ordenado -. Si se considera el orden como inverso; es decir que el primer símbolo es aquél que se escribe primero, la fórmula correspondiente es la (2). Pero la idea es la misma.

Operaciones

La operación de adición (suma) es bastante simple en este tipo de sistemas. Sólo hay que tener en cuenta el orden del conjunto de la base, y que al llegar hasta el último símbolo vuelvo al principio y agrego una unidad al orden superior ('me llevo una').

En el Sistema Decimal sería:
0->1->2->3->4->5->6->7->8->9->0 (y me llevo 1) y puedo volver a empezar.

Pero puedo generalizarlo a cualquier sistema de numeración cuyo último símbolo sea & y el primero sea 0
0-> · · · ->&->0 (y me llevo 1) y puedo volver a empezar

Por ejemplo, en el sistema hexadecimal: 2D6B + 9356

Como el sistema hexadecimal los símbolos son {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} podría hacer 6 saltos desde el símbolo B según el orden de la base: B->C->D->E->F->0->1. Por lo que quedaría 1 y me llevo 1 al siguiente.

Otra forma de hacerlo, más larga pero menos confusa, es pasando todo al sistema decimal que se supone manejamos bien:
6 + B = 6 + 11 = 17 = 11 (en base 16) que es lo que dijimos antes: queda 1 y me llevo otra al orden superior.

Así, la operación completa sería:

6+B = 16 + 1 --> ---1
5+6+1 = 12 --> --C1
D+3 = 16 + 0 --> -0C1
9+2+1= 12 --> C0C1

(continúa...)

P.D.: Esto es un boceto de lo que tengo pensado para ese apunte que alguna vez mencioné. Acepto críticas de todo tipo."